Physics Notes Form 3
Physics Notes Form 3
Physics Form Three
Chapter One
Linear Motion
Introduction
Study of motion is divided into two;
1. Kinematics
2. Dynamics
In kinematics forces causing motion are disregarded while dynamics deals with motion of objects and the forces causing them.
I. Displacement
Distance moved by a body in a specified direction is called displacement. It is denoted by letter‘s’ and has both magnitude and direction. Distance is the movement from one point to another. The Si unit for displacement is the metre (m).
II. Speed
This is the distance covered per unit time.
Speed= distance covered/ time taken. Distance is a scalar quantity since it has magnitude only.
The SI unit for speed is metres per second(m/s or ms-1)
Average speed= total distance covered/total time taken Other units for speed used are Km/h.
Examples
1. A body covers a distance of 10m in 4 seconds. It rests for 10 seconds and finally covers a distance of 90m in 60 seconds. Calculate the average speed.
Solution
Total distance covered =10+90= 100m
Total time taken =4+10+6= 20 seconds
Therefore average speed = 100/20= 5m/s
2. Calculate the distance in metres covered by a body moving with a uniform speed of 180 km/h in 30 seconds.
Solution
Distance covered=speed*time
=180*1000/60*60=50m/s
=50*30
=1,500m
3. Calculate the time in seconds taken a by body moving with a uniform speed of 360km/h to cover a distance of 3,000 km?
Solution
Speed:360km/h=360*1000/60*60=100m/s
Time=distance/speed
3000*1000/100
=30,000 seconds.
III. Velocity
This is the change of displacement per unit time. It is a vector quantity.
Velocity=change in displacement/total time taken
The SI units for velocity are m/s
Examples
1. A man runs 800m due North in 100 seconds, followed by 400m due South in 80 seconds. Calculate,
a. His average speed
b. His average velocity
c. His change in velocity for the whole journey
Solution
a. Average speed: total distance travelled/total time taken
=800+400/100+80
=1200/180
=6.67m/s
b. Average velocity: total displacement/total time
=800-400/180
=400/180
=2.22 m/s due North
c. Change in velocity=final-initial velocity
= (800/100)-(400-80)
=8-5
=3m/s due North
2. A tennis ball hits a vertical wall at a velocity of 10m/s and bounces off at the same velocity. Determine the change in velocity.
Solution
Initial velocity(u)=-10m/s
Final velocity (v) = 10m/s
Therefore change in velocity= v-u
=10- (-10)
=20m/s
IV. Acceleration
This is the change of velocity per unit time. It is a vector quantity symbolized by ‘a’. Acceleration ‘a’=change in velocity/time taken= v-u/t The SI units for acceleration are m/s2 Examples 1. The velocity of a body increases from 72 km/h to 144 km/h in 10 seconds.
Calculate its acceleration.
Solution
Initial velocity= 72 km/h=20m/s
Final velocity= 144 km/h=40m/s
Therefore ‘a’ =v-u/t
= 40-20/10
2m/s2
2. A car is brought to rest from 180km/h in 20 seconds. What is its retardation?
Solution
Initial velocity=180km/h=50m/s
Final velocity= 0 m/s
A = v-u/t=0-50/20
= -2.5 m/s2
Hence retardation is 2.5 m/s2
Motion graphs
Distance-time graphs
a)
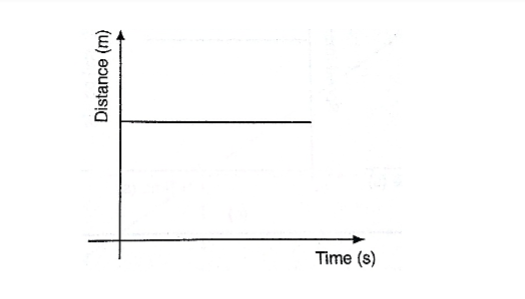
b)
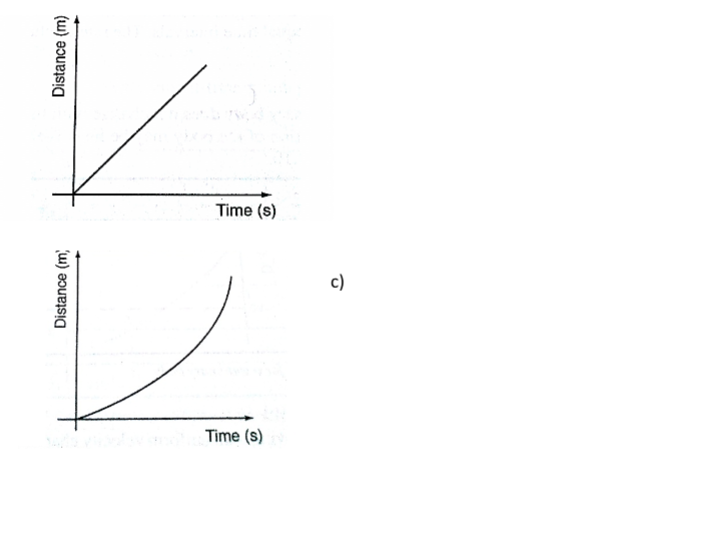
Area under velocity-time graph
Consider a body with uniform or constant acceleration for time‘t’ seconds;
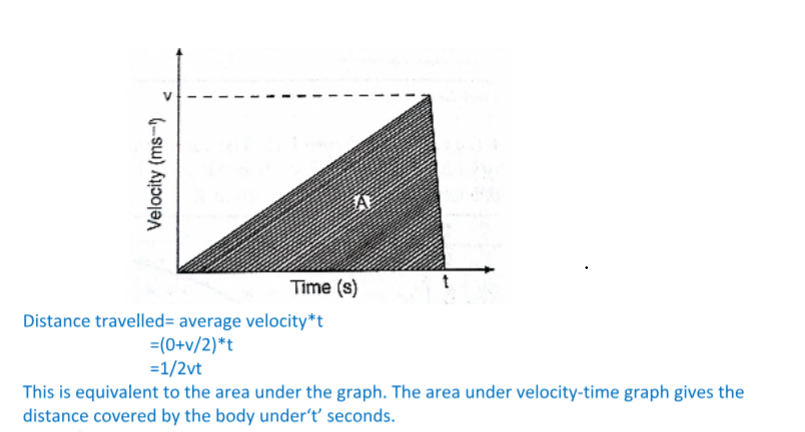
This is equivalent to the area under the graph. The area under velocity-time graph gives the distance covered by the body under‘t’ seconds.
Example
A car starts from rest and attains a velocity of 72km/h in 10 seconds.
It travels at this velocity for 5 seconds and then decelerates to stop after another 6 seconds.
Draw a velocity-time graph for this motion. From the graph;
i. Calculate the total distance moved by the car
ii. Find the acceleration of the car at each stage.
Solution
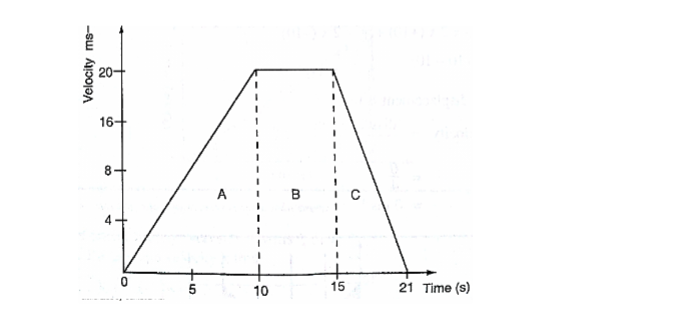
a. From the graph, total distance covered= area of (A+B+C)
=(1/2×10×20)+(1/2×6×20)+(5×20)
=100+60+100
=260m
Also the area of the trapezium gives the same result.
b. Acceleration= gradient of the graph
Stage A gradient= 20-0/ 10-0 = 2 m/s2
Stage b gradient= 20-20/15-10 =0 m/s2
Stage c gradient= 0-20/21-15 =-3.33 m/s2
Using a ticker-timer to measure speed, velocity and acceleration. It will be noted that the dots pulled at different velocities will be as follows;
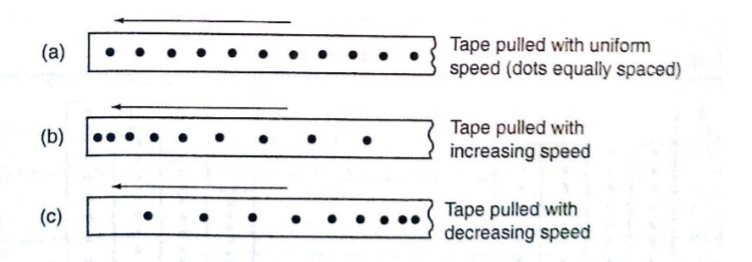
Most ticker-timers operate at a frequency of 50Hzi.e. 50 cycles per second hence they make 50 dots per second. Time interval between two consecutive dots is given as,
1/50 seconds= 0.02 seconds. This time is called a tick.
The distance is measured in ten-tick intervals hence time becomes 10×0.02= 0.2 seconds.
Examples
a. A tape is pulled steadily through a ticker-timer of frequency 50 Hz.
Given the outcome below, calculate the velocity with which the tape is pulled.
Solution
Distance between two consecutive dots= 5cm
Frequency of the ticker-timer=50Hz
Time taken between two consecutive dots=1/50=0.02 seconds
Therefore, velocity of tape=5/0.02= 250 cm/s
b. The tape below was produced by a ticker-timer with a frequency of 100Hz. Find the acceleration of the object which was pulling the tape.

Solution
Time between successive dots=1/100=0.01 seconds
Initial velocity (u) 0.5/0.01 50 cm/s
Final velocity (v) 2.5/0.01= 250 cm/s
Time taken= 4 ×0.01 = 0.04 seconds
Therefore, acceleration= v-u/t= 250-50/0.04=5,000 cm/s2
Equations of linear motion
The following equations are applied for uniformly accelerated motion;
v = u + at
s = ut + ½ at2
v2= u2 +2as
Examples
1. A body moving with uniform acceleration of 10 m/s2 covers a distance of 320 m. if its initial velocity was 60 m/s. Calculate its final velocity.
Solution
V2 = u2 +2as
= (60) +2×10×320
=3600+6400
= 10,000
Therefore v= (10,000)1/2
v= 100m/s
2. A body whose initial velocity is 30 m/s moves with a constant retardation of 3m/s. Calculate the time taken for the body to come to rest.
Solution
v = u+at
0= 30-3t
30=3t
t= 30 seconds.
3. A body is uniformly accelerated from rest to a final velocityof 100m/s in 10 seconds. Calculate the distance covered.
Solution
s=ut+ ½ at2
=0×10+ ½ ×10×102
= 1000/2=500m
Motion under gravity.
1. Free fall
The equations used for constant acceleration can be used to become,
v =u+gt
s =ut + ½ gt2
v2= u+2gs
2. Vertical projection
Since the body goes against force of gravity then the following equations hold
v =u-gt ……………1
s =ut- ½ gt2 ……2
v2= u-2gs …………3
N.B time taken to reach maximum height is given by the following
t=u/g since v=0 (using equation 1)
Time of flight
The time taken by the projectile is the timetaken to fall back to its point ofprojection. Using eq. 2 then, displacement =0
0= ut- ½ gt2
0=2ut-gt2
t(2u-gt)=0
Hence, t=0 or t= 2u/g
t=o corresponds to the start of projection
t=2u/gcorresponds to the time of flight
The time of flight is twice the time taken to attain maximum height.
2024 FORM 1 2 3 4 REVISION RESOURCES
FORM 1 2 3 4 TERM 1 2 3 OPENER , MID AND END TERM EXAMS
1995-2024 KCSE KNEC PAPERS QUESTIONS,ANSWERS AND REPORT
2008-2024 KCSE FORM 4 COUNTY MOCKS
FORM 1 2 3 4 SCHEMES OF WORK
FORM 1 2 3 4 LESSON PLANS
FORM 1 2 3 4 CLASS REVISION NOTES
FORM 1 2 3 4 TERM 1 2 3 HOLIDAY ASSISNMENTS
FORM 3 4 SETBOOKS STUDY GUIDES
FORM 1 2 3 4 TOPICAL TESTS
FORM 1 2 3 4 REVISION BOOKLETS
LIFE SKILLS NOTES
FORM 1 2 3 4 SYLLABUS
KENYA SCHOOL CODES
HOW TO REVISE AND PASS EXAMS
GUIDANCE AND CONSELLING NOTES
CLICK HERE TO DOWNLOAD ALL LATEST 2024 KCSE REVISION MOCKS
KCSE COUNTY MOCKS DOWNLOADS 2024
2023 KCSE COUNTY MOCKS DOWNLOADS
- 2023 KAPSABET BOYS POST MOCK
- PANGANI MOCK KCSE 2023
- KCSE 2023 LAINAKU II FORM 4 JOINT MOCK
- KENYA HIGH POST MOCK
- KALA MOCK =Password is- subjectcodeKALA2023
- KCSE 2023 SAMIA JOINT MOCK
LANJET 2023 EVALUATION MOCK
2023 EVALUATION MOCK nyandarua trial 4
2023 EVALUATION MOCK nyandarua trial 3
KCSE 2023 MOCKS NYARIRA CLUSTER EXAMS
KCSE 2023 CEKANA MOCKS
KCSE 2023 ACHIEVERS JOINT MOCK
- KAPSABET 2 MOCK 2023
- MOKASA 2 MOCK 2023
- 2023 Mang’u high revision mock
- FORM 4 TERM 2 BAKALE EXAM
CATHOLIC DIOCESE OF KAKAMEGA MOCK
- BSJE JOINT MOCK EXAM 2023
- MARANDA HIGH SCHOOL MOCK JUNE
- KCSE 2023 mock Nginda girls
- 2023 Kcse mock Wahundura
- 2023 Kcse mock set 22
KCSE 2023 KASSU MOCK EXAMS
- 2023 KCSE EAGLE TRIAL 1 MOCK
- 2023 lainaku revision mock
- 2023 FORM 4 evaluation exams set 18
- 2023 FORM 4 evaluation exams set 17
- 2023 FORM 4 evaluation exams set 16
LUGARI CONSTITUENCY -MOCK 1
- 2023 KCSE FORM 4 EVALUATION TEST
2023 mokasa mocks revision exams
- SUKELLEMO JOINT PRE-MOCK EXAMS
- Mumias west pre mock kcse exams
- 2023 SUNRISE PRE-MOCK
- 2023 kcse arise and shine pre-mock
- MECS CLUSTER JOINT MOCK EXAM
- Chogoria murugi zone pre-mock
- MOMALICHE 2 EXAMS PRE MOCK
- ASUMBI PRE MOCK EXAMS 2023
- 2023 MARANDA HIGH PRE-MOCK
- KAPSABET INTERNAL TRIAL 1 2023
- FORM 4 EVALUATION TEST 2023
- 2023 FORM 4 evaluation exams
Mock exams and pre-mock exams are practice tests that are taken before the actual exams.
2022 COUNTY MOCKS 38 EXAMS
2021-22 COUNTY MOCKS 36 EXAMS
2020-21 COUNTY MOCKS 24 EXAMS
2019 COUNTY MOCKS 44 EXAMS
2018 COUNTY MOCKS 23 COUNTIES EXAMS
2017 COUNTY MOCKS 25 COUNTIES EXAMS
2016 COUNTY MOCKS 16 COUNTIES
2015 COUNTY MOCKS 20 COUNTIES
2008 , 2009 , 2010 , 2011 , 2012 , 2013, 2014 COUNTY MOCKS 25 COUNTIES
2023 KCSE COUNTY MOCKS Mock exams and pre-mock exams are practice tests that are taken before the actual exams.
They are designed to help students get a sense of what to expect in the real exam and to identify areas where they need to improve.
The purpose of taking mock exams is to help students build confidence, develop test-taking strategies, and identify their strengths and weaknesses.
Pre-mock exams are usually taken a few weeks or months before the actual exam, while mock exams are usually taken closer to the exam date.
 WhatsApp us Now
WhatsApp us Now